1. 미분 공식
미분은 곱셈 공식처럼 다음과 같은 공식이 있습니다.
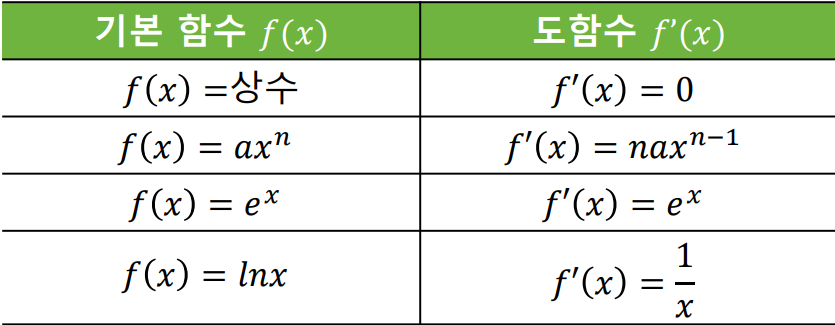
f(x)가 상수라면 미분 했을때 0이 나오고,
f(x)가 ax^n이라면 n과 ax를 곱해주고 지수 n에는 -1을 해줍니다.
f(x)가 e^x라면 그대로 자기 자신이 나오게 됩니다.
f(x)가 lnx(여기서 ln은 자연로그)라면 1/x이 나옵니다.
예를 들어 다음과 같은 식이 있을때 미분 공식으로 미분하면 어떻게 나오는지 계산해보겠습니다.
$$f\left( x\right) =3x^{2}+e^{x}+7$$
$$f'\left( x\right) =2\times 3x+e^{x}+0=6x+e^{x}$$
즉, 6x+e^x가 미분 계수가 됩니다.
$$f\left( x\right) =\ln x+\dfrac{1}{x}$$
위와 같은 식이 있다면 이를 미분했을때 다음과 같은 결과가 나옵니다.
$$f'\left( x\right) =\dfrac{1}{x}+\left( -1x^{-2}\right) =\dfrac{1}{x}-\dfrac{1}{x^{2}}$$
여기서 1/x^2가 나오는 이유는 1/x를 미분 공식에 대입하면 1/x는 x의 -1제곱이므로
-1을 곱해주고 지수에는 -1을 해주므로 지수는 -2가 됩니다.
x의 -2제곱은 1/x^2입니다.
2. 편미분
편미분은 입력 변수가 2개 이상인 다변수 함수에서 미분하고자 하는 변수 1개를 제외한
나머지 변수들은 상수로 취급하고, 특정한 한 변수에 대해서만 미분하는 것을 의미합니다.
예를 들어 f(x,y)를 변수 x에 대해 편미분 하는 경우 다음과 같이 대수적으로 나타냅니다.
$$\dfrac{\partial f\left( x,y\right) }{\partial x}$$
여기서 a는 라운드를 뜻하며 위 대수적 표현의 뜻은 f(x,y)를 x에 대해 편미분 하겠다는 뜻입니다.
$$\left( x,y\right) =2x+3xy+y^{3}$$
f(x,y)가 위와 같을 때 각각 x와 y의 대한 편미분을 해보겠습니다.
먼저 x에 대한 편미분입니다.
$$\dfrac{\partial \left( 2x+3xy+y^{3}\right) }{\partial x}=2x+3y$$
2x는 미분 공식에 따라 1*2x^0이므로 x의 0제곱은 1 따라서 2x 그대로 나오게 됩니다.
3xy는 3y*x라고 생각하시면 됩니다.
여기서 x는 1*x^0이므로 3y * 1은 3y 따라서 3xy는 3y입니다.
마지막으로 y^3은 상수항으로 생각하므로 상수의 미분은 0이니 y^3은 0입니다.
y에 대한 편미분입니다.
$$\dfrac{\partial \left( 2x+3xy+y^{3}\right) }{\partial y}=3x+3y^{2}$$
2x는 x를 상수항으로 생각하므로 0
3xy는 y가 1*y^0이므로 3x*1 = 3x이니 3x
y^3은 3* y^2이므로 3y^2입니다.
다음 포스트는 곱의 미분과 체인룰에 대해 알아보겠습니다.
'머신러닝' 카테고리의 다른 글
| [파이썬] 합성함수, 체인 룰 , 수치 미분 (0) | 2023.05.18 |
|---|---|
| [파이썬] boston 집 값 예측 ( 결정트리 회귀, 랜덤 포레스트 회귀 ) (0) | 2023.05.16 |
| [인공지능 수학] 미분의 정의 (0) | 2023.05.10 |
| [파이썬] 의사결정 트리( DecisionTree ) (0) | 2023.05.03 |
| [파이썬] 역행렬과 유사역행렬 (0) | 2023.04.20 |



